System Architecture
Architectural approaches, microservices/monolith, sync/async, atomic/eventual
The conference is dedicated to practical software architecture. Our speakers include engineers from the world's leading companies.

Architectural standards and frameworks, analysis of requirements, architecture documentation, assessment of architecture

AWS / Google Cloud / Azure, cloud services, serverless, no code, cloud cost optimization
We invite you to participate in the International Conference of Software Quality Assurance Specialists. As always, the conference will cover a wide range of professional issues in the field of quality assurance, the key ones being
For many specialists and managers, the XI Vero Software Conference is a real opportunity to make themselves known, to raise the professional level of employees who are responsible for software and, thus, to strengthen the competitive position and create an advantage. XI Vero is a wonderful platform of communication and experience exchange for people involved in the sphere of software testing.
Book a Ticket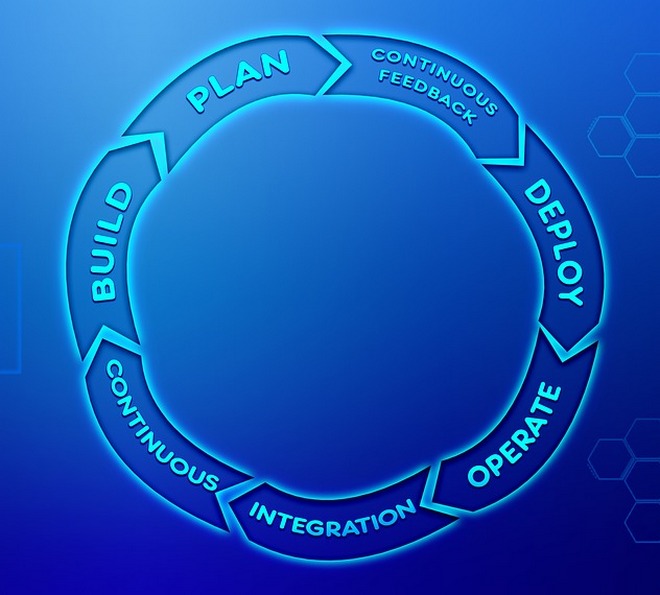
Writing a great code is difficult, but it is even more difficult to make correct decisions during its development. How can you apply Domain Driven Design to your monolith and how can you apply it to microservices?
We will implement the architectural catalogs for the requested business case. We will look at ADD in detail. How does the document looks architecture vision.
So, you have some things that you want to change in your servers without redeploying them. There are some mappings or feature toggles.

Investment platform software https://tesla-coin.tech/
 GetDevDone – white label web development service for small and medium digital and marketing agencies. Deliver the web dev projects for your clients on time and on budget.
GetDevDone – white label web development service for small and medium digital and marketing agencies. Deliver the web dev projects for your clients on time and on budget.

Development of indoor tracking solutions for your business. Track the movement of objects, assets indoors.

Development of applications for neobanks that will allow your fintech project to keep up with the times.
 Here you will learn how to create a business app and get the most out of it. Read the article, and you will understand what it takes to build a business app and what influences success.
Here you will learn how to create a business app and get the most out of it. Read the article, and you will understand what it takes to build a business app and what influences success.  Stigan Media is a team of cannabis SEO experts. We specialize in helping cannabis businesses grow their SEO traffic and increase their profits.
Stigan Media is a team of cannabis SEO experts. We specialize in helping cannabis businesses grow their SEO traffic and increase their profits.  Achieve top search results and enhance your visibility with the strategic insights from our Seodach – SEO agency in Munich.
Achieve top search results and enhance your visibility with the strategic insights from our Seodach – SEO agency in Munich.






We will look at the types of errors in the approaches to the design of large systems, which lead to serious or even catastrophic consequences for business.

Let's talk about architecture in BigTech, technology selection and accepted "rules". We will touch on the topic of freedom in adopting architectural solutions for the Product and Core teams.

We encounter the Apache Cassandra database and the need to operate it as part of a Kubernetes-based infrastructure on a regular basis. In this piece, we will share our view of the necessary steps, criteria and existing solutions (including a review of operators) for migrating Cassandra to K8s.
People frequently record their regular training activities to live a physically healthy life and move forward in it.